Julie Fisher

Julie Fisher

Problem solver extraordinaire applying critical thinking through data science.

Entry 42: Logistic Regression

5 minute read

Page 143 of Hands-On Machine Learning with Scikit-Learn, Keras, and TensorFlow states that Logistic Regression is “just like a Linear Regression model” except that “instead of outputting the result directly like the Linear Regression model does, it outputs the logistic of this result.”

The notebook where I did my code for this entry can be found on my github page in the Entry 42 notebook.

Learning Style

Supervision Prediction types
Supervised Classification

Description

Logistic Regression adds a sigmoid function to linear regression, which allow it to make classification predictions. I covered the linear regression equations in Entry 35, but as a reminder:

$\hat{y} = h_{0}(x) = \theta_{0} + \theta_{1}x_{1} + \theta_{2}x_{2} + \dotsb + \theta_{n}x_{n} = \theta^{T} x$

Where

  • $h_{\theta}$: prediction function, also called a hypothesis; $h_{\theta} = \theta^{T}x^{(i)}$
  • $\theta$: vector (i.e. list) of weights, with the first value being the y-intercept type value (represented by b in Introduction to Machine Learning)
  • $x$: the matrix of feature values (i.e. the DataFrame) with the first column ($x_{0}$, not listed in the equation) being all 1s so that $\theta_{0}$ is always evaluated as the same value

The addition of the sigmoid function turns the output into a number between 0 and 1, where the predictions form an S-shape.

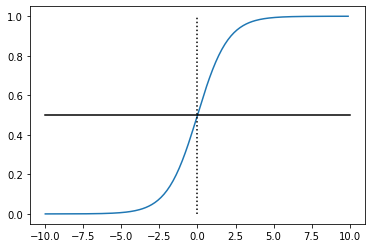
Logistic S Curve

Hands-On Machine Learning spells out the importance of this on page 143. The output is “the probability $\hat{p} = h_{\theta}(x)$ that an instance $x$ belongs to the positive class.” From there, it’s easy to turn into a classification prediction:

$\hat{y} = \begin{cases} 0 \text{ if } \hat{p} < 0.5 \newline 1 \text{ if } \hat{p} \geq 0.5 \end{cases}$

The above assumes that the desired threshold is 0.5. I covered choosing thresholds in Entry 26. In Logistic Regression, the threshold is also called the “decision boundary” because the threshold marks the boundary between a “yes” or “no” decision.

Purpose

The purpose of Logistic Regression is to apply the same mathematical principles as Linear Regression to classification problems. By that I mean, Logistic Regression still finds linear patterns in the data.

To make the linear regression equation into a logistic regression equation, a sigmoid function is added:

$h_{0}(x) = g(\theta^{T}x) = g(z) = \frac{1}{1+e^{-z}} = \frac{1}{1+e^{-\theta^{T}x}}$

Where:

  • $z = X \theta = \theta^{T}x$
    • (m x n) x (n x 1 ) = (m x 1)
  • e = Euler’s number (i.e. the base of natural logarithm)
    • The exact value is in the math library: math.e
    • To use it in this equation, math.exp(-z)
  • g = sigmoid function

The above equations came from week 3 of Andrew Ng’s Machine Learning course.

Inputs to the sigmoid function that are higher will be closer to 1 and those that are lower will be closer to 0.

Behavior

Because Logistic Regression is essentially Linear Regression with a sigmoid function, it behaves very similarly to Linear Regression.

These similarities include:

  • The classes are separated by a line, plane or hyperplane (The Behavior section of Entry 35 has illustrations of this concept)
  • Regularization can be applied (Scikit’ LogisticRegression function applies L2 regularization by default. I cover L1 and L2 regularization in Entry 38)
  • Gradient Descent is used to find the global minimum (I cover Gradient Descent in Entry 37b)

On page 144 of Hands-On Machine Learning with Scikit Learn, Aurelien points out a notable exception to the similarities: Logistic Regression has no equivalent to the Normal Equation (I cover Normal Equation in Entry 37a). Gradient Descent is the method used to determine the cost function and find the best fit to the data.

Introduction to Machine Learning with Python also warns on page 58 that:

LogisticRegression is a classification algorithm and not a regression algorithm, and it should not be confused with LinearRegression.

Multiple Classes

On page 148 of Hands-On Machine Learning with Scikit Learn, Aurelien discusses using Logistic Regression to predict on multiple classes (i.e. more than binary “yes”/”no” decisions) using Softmax Regression.

As I don’t work with multi-class predictions, I’ll be skipping Softmax.

Parameters

Scikit Learn has 15 parameters, all of which have default parameters.

  • penalty=’l2’
  • dual=False
  • tol=0.0001
  • C=1.0
  • fit_intercept=True
  • intercept_scaling=1
  • class_weight=None
  • random_state=None
  • solver=’lbfgs’
  • max_iter=100
  • multi_class=’auto’
  • verbose=0
  • warm_start=False
  • n_jobs=None
  • l1_ratio=None

The full descriptions of what each does is available on the Scikit Learn LogisticRegression page, but I want to call out two here.

As mentioned above in the Behavior section, L2 regularization is applied by default. Introduction to Machine Learning with Python points out on page 64 that this can be changed to L1 regularization if a more interpretable model is desired, as it uses fewer features (L1 and L2 regularization are covered in Entry 38).

The second parameter is C. Both Hands-On Machine Learning with Scikit Learn and Introduction to Machine Learning with Python spend several paragraphs talking about this parameter. It controls the amount of regularization. The important thing to remember about C is that it the inverse of regularization strength. Higher values of C produce less regularization. As such, if the model needs more regularization, start using decimal values like 0.01.

Strengths

  • Fast to train
  • Fast to predict
  • Easily scale to very large datasets
    • On page 263 Machine Learning with Python Cookbook discusses using the stochastic average gradient (SAG) solver on large datasets
    • The large dataset discussion includes a warning that SAG is very sensitive to feature scaling, so standardizing the features is extremely important
  • Works well with sparse data
  • Performs well when the number of features is large compared to the number of observations (ex, 104 features but only 5 observations)
  • Handles imbalanced classes using the class_weight parameter (I discuss imbalanced classes in Entry 23)

Limitations

  • In low dimensions, logistic models appear to have very limited usefulness. However, as more dimensions are added, the model becomes more powerful and can become overfit
  • Specializes in linear relationships
    • While features can be augmented to help capture curvilinear relationships (like quadratic or cubic), Logistic Regression may not adequately capture nonlinear relationships
    • Adding additional features to augment curvilinear relationships can create or exacerbate model overfitting
  • As it uses the mean of the residuals, it is susceptible to outliers
  • May become erratic when the number of predictors is higher than the number of observations (ex, 14 features but only 5 observations)

Up Next

NODES2020 Graph Visualization Talk

Resources

You May Also Enjoy

Entry SM02: Clean Data

19 minute read

Wrangling data into a usable form is a big part of any real world machine learning problem. When tackling these types of problems, several things are general...

Entry SM01: Using S3 from AWS’s SageMaker

10 minute read

There are a lot of considerations in moving from a local model used to train and predict on batch data to a production model. This series of posts explores h...

Entry NLP4: Frequencies and Comparison

26 minute read

In the previous entries in this series, I loaded all the files in a directory, processed the data, and transformed it into ngrams. Now it’s time to do math a...