Entry 40: Ridge Regression
Ridge Regression is a form of regression regularization using L2 regularization.
The notebook where I did my code for this entry can be found on my github page in the Entry 40 notebook.
Learning Style
| Supervision | Prediction types |
|---|---|
| Supervised | Regression |
| Classification |
Description
This method similar to Lasso Regression Entry 39 in that it uses the same formula as OLS and minimizes the magnitude of coefficients (w), but instead of using L1 regularization, Ridge Regression uses L2 regularization.
Ridge Regression minimizes the magnitude of coefficients (w). Basically, it tries to keep the weights (w) as close to zero as possible. Introduction to Machine Learning with Python states on page 51 that:
Intuitively, this means each feature should have as little effect on the outcome as possible (which translates to having a small slope), while still predicting well.
Purpose
On pages 135 and 137, Hands-On Machine Learning with Scikit-Learn provides the following two updated equations from the OLS linear regression versions:
- Cost function: $J(\theta) = MSE(\theta) + \alpha \frac{1}{2} \displaystyle\sum_{i=1}^n \theta_{i}^{2}$
- Note: The bias term $\theta_{0}$ is not regularized as indicated by the start of $i$ at 1 instead of 0
- Where
- MSE: mean squared error
- $\alpha$: regularization term
- i.e. how much the model is regularized
- A value of 0 is no regularization (i.e. regular linear regression)
- As the value approaches infinity, the weights approach zero (i.e. no features contribute and results in a flat line through the data’s mean)
- $\theta$: the theta array
- Vectorized ridge regression: $\hat{\theta} = (X^{T} X + \alpha A)^{-1} X^{T}y$
- Where
- $\theta$: the theta array
- $X$: the feature matrix
- $X$: the transpose of the feature matrix
- $\alpha$: the regularization term
- i.e. how much the model is regularized
- A value of 0 is no regularization (i.e. regular linear regression)
- As the value approaches infinity, the weights approach zero (i.e. no features contribute and results in a flat line through the data’s mean)
- $A$: the identify matrix, except with the top-left cell being 0 (i.e. the bias term)
- $y$: the target array
- Where
Behavior
The outcome of keeping the coefficients as small as possible helps reduce the complexity of the model (i.e. makes it more generalized and reduces overfitting). The complexity of the model is controlled through the parameter alpha. Larger values of alpha force the coefficients closer to 0 (reducing complexity), smaller values of alpha are less restricting (allowing for more complexity).
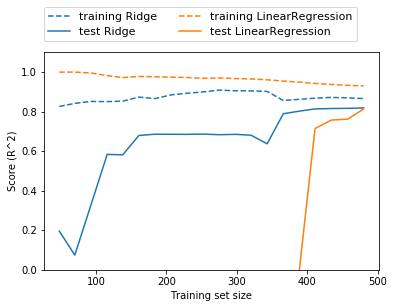
As seen in the chart below from Introduction to Machine Learning with Python’s mglearn package, Ridge Regression gets lower scores than Linear Regression on training data, but higher scores on the test data.
Ridge Regression can also be used on smaller sample sizes than Linear Regression. However, the scores for Ridge Regression and Linear Regression converge once the training dataset reaches a certain size (the convergence point will vary from dataset to dataset).
Parameters
alpha
Strengths
Introduction to Machine Learning with Python pointed out on page 52 that forcing coefficients toward 0 will decrease performance on the training set. However, if the model is overfitting, restricting the coefficients will help improve model performance on the test data (and since the goal of machine learning is to predict well on data that’s never been seen, not the data that it was trained on, this is a good thing).
- Minimizes variance
Limitations
- No automatic reduction of features
